CHAPTER 4: DIGITAL LOGIC
Basic Revision At Logic Gate

Digital systems are said to be constructed by using logic gates. These gates are the AND, OR, NOT, NAND, NOR, XOR gates.

      

AND

  

       OR

      

   NOT

  

  

  

NAND

 NOT-AND gate which is equal to an AND gate followed by a NOT gate.

  

  

 NOR

 NOT-OR gate which is equal to an OR gate followed by a NOT gate

  

 XOR

The 'Exclusive-NOR' gate circuit does the opposite to the OR gate.

  

Basic Combination Circut 

There were three ways we can use to do a combination circut:

1) Truth table

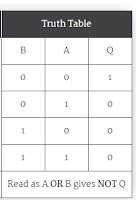
 Truth table helps we to understand the inputs of logic gate, We can know what the input and output

The gate input(s) are shown in the left column(s) of the table with all the different possible input combinations. This is normally done by making the inputs count up in binary.

Truth tables list-out the output of a particular digital logic circuit for all the possible combinations of its inputs.

2) Graphical Symbols

This is a graphic symbols that we use to present the operation of logic gate.  

3)Boolean equation

Description of the Laws of Boolean Algebra

Annulment Law – A term AND´ed with a “0” equals 0 or OR´ed with a “1” will equal 1.
•  
  A . 0 = 0 A variable AND’ed with 0 is always equal to 0.
  
  
  A + 1 = 1 A variable OR’ed with 1 is always equal to 1.
•  
Identity Law – A term OR´ed with a “0” or AND´ed with a “1” will always equal that term.
•  
  A + 0 = A A variable OR’ed with 0 is always equal to the variable.
  
  
  A . 1 = A A variable AND’ed with 1 is always equal to the variable.
•  
Idempotent Law – An input that is AND´ed or OR´ed with itself is equal to that input.

    A + A = A A variable OR’ed with itself is always equal to the variable.
    A . A = A A variable AND’ed with itself is always equal to the variable.

•  
Complement Law – A term AND´ed with its complement equals “0” and a term OR´ed with its complement equals “1”.

     A . A = 0 A variable AND’ed with its complement is always equal to 0.
     A + A = 1 A variable OR’ed with its complement is always equal to 1.

Commutative Law – The order of application of two separate terms is not important.

    A . B = B . A The order in which two variables are AND’ed makes no difference.
    A + B = B + A The order in which two variables are OR’ed makes no difference.
•  
Double Negation Law – A term that is inverted twice is equal to the original term.

    A = A A double complement of a variable is always equal to the variable.

        

 Example:       Using the above laws, simplify the following expression: (A + B)(A + C)

"de Morgan´s Theorem"  There are two “de Morgan´s” rules or theorems,

             (1) Two separate terms NOR´ed together is the same as the two terms inverted (Complement)               and AND´ed for example, A+B = A. B.

               (2) Two separate terms NAND´ed together is the same as the two terms inverted                                (Complement) and 'OR´ed for example, A.B = A +B.

    Karnaugh Map

   A Karnaugh Map is a grid-like representation of a truth table. It is really just another way of presenting a truth table, but the mode of presentation gives more insight

    

The Karnaugh Map is a visual technique that allows you to generate groupings of terms that can be combined with a simple visual inspection

Note the following about the four variable Karnaugh Map.

   

               There are 16 cells in the map. Anytime you have N variables, you will have 2N possible                                      combinations, and 2N places in a truth table or Karnaugh Map.

Imagine moving around in the Karnaugh Map. Every time you cross a horizontal or vertical boundary one - and only one - variable changes value.

The two pairs of variables - WX and YZ - both change in the same pattern.

Example:

Universal Gates

Universal gates that caan be used to implement any gates like AND, OR ,NOT, and any combination of gates. NAND and  NOR are the  universal gates.

NAND

We will consider the truth table of the above NAND gate i.e. a two-input gate. The two inputs are A and B.


         

List of NAND gates. 

NOR

The above diagram is of an OR gate made by only using NOR gates. The output of this gate is exactly similar to that of a single OR gate. As we can see the circuit arrangement of OR gate using NOR gates.

There not many different between NAND and NOR gates.

The Logic NOR Gate or Inclusive-NOR gate is a combination of the digital logic OR gate with that of an inverter or NOT gate connected together

The NOR (Not – OR) gate has an output that is normally at logic level “1” and only goes “LOW” to logic level “0”

 There are have a few ways to show the input:

2-input NOR Gate 

                

                                                        

 

3-input NOR