CHAPTER 2 : NUMBER SYSTEM

BASIC TYPE OF NUMBER SYSTEM

A number system is a basic symbol to represent a set of quantities . There are many types of number system . Here we only focus on the decimal , hexadecimal , and binary number .

DECIMAL           BINARY       HEXADECIMAL
      0                      0000                       0
      1                      0001                       1
      2                      0010                       2
      3                      0011                       3
      4                      0100                       4
      5                      0101                       5
      6                      0110                       6
      7                      0111                       7
      8                      1000                       8
      9                      1001                       9
    10                      1010                       A
    11                      1011                       B
    12                      1100                       C
    13                      1101                       D
    14                      1110                       E
    15                      1111                       F



C0NVERT DECIMAL TO BINARY





CONVERT DECIMAL TO HEXADECIMAL





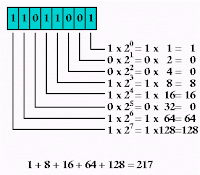
CONVERT BINARY TO DECIMAL




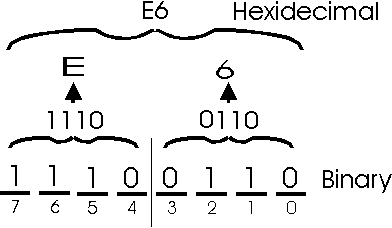
CONVERT BINARY TO HEXADECIMAL



CONVERT HEXADECIMAL TO DECIMAL




CONVERT HEXADECIMAL TO BINARY



2 COMPLEMENT NUMBER

In microprocessor - based equipment , 2s complement method of representing numbers is commonly used . Untill now , we only assume that the number are positive . However , microprocessor must process both positive and negative number . The 2s complement representation used for sign and magnitude number can be determined .

Assume a microprocessor have 8 register bits . Figure 2-1 show the sign bits or the most significant bit (MSB) . If the MSB bit is 0 , then the number is positive (+) . Cconversely , if the MSB is 1 , then the number is negative (-) . The others remaining 7 bits are represent as the magnitude numbers . The first bit from right is a leasr significant bit (LSB).

SIGN BIT 0 = (+)

                 1 = (-)

MSB

LSB

                                                                   MAGNITUDE

EXAMPLE :-

DECIMAL	8-BIT     BINARY NUMBER			NOTE
	SIGN	MAGNITUDE
125	0	111 1101	CONVERT TO 7 BIT BINARY
		000 0010	1st complement	Each 0 is changed to a1 and each 1 to a 0
		000 0011	2nd complement	Add + 1 to the 1st complement
-125	1	000 0011	7-bit 2nd complement	Magnitude number